| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- ddpm
- unconditional ddpm
- linear inverse problem
- ccdf
- image restoration
- Ai
- conditional diffusion
- ddim
- IR
- ML
- semi-supervied learning
- object detection
- ssda-yolo
- diffpir
- ddrm
- fourmer
- neighboring pixel relationships
- diffusion
- facenet
- face forgery detection
- focal detection network
- hqs-algorithm
- Triplet
- daod
- ilvr
- f2dnet
- deepfake detection
- pedestrian detection
- stochastic contraction theory
- unconditional generative models
- Today
- Total
Stand on the shoulders of giants
[paper review] DDRM (Denoising Diffusion Restoration Models) 본문
[paper review] DDRM (Denoising Diffusion Restoration Models)
finallyupper 2024. 7. 6. 10:37Introduction
본 논문은 Image restoration(IR)에서의 linear inverse problems를 해결하기 위해 제안된 unsupervised posterior sampling 방법론으로, pre-trained denoising diffusion generative model을 활용한다. 학습된 priors에 기반한 unsupervised 접근들의 경우 재학습 없이 새로 주어지는 문제에 adapt할 수 있기에 supervised보다 desirable하다.
signal을 복원하기위해 보통의 방법론들은 아래 과정을 따른다.
[1] Prior-related terms over the signal
- Neural network를 통해 distribution 등의 정보 획득
- degradation model로부터 likelihood 획득
⇒ 두 term을 가지고 posterior를 구하고자 한다.
[2] Posterior
이때의 Inverse problem
- Optimization problem
- Solving a sampling problem
[3] posterior를 형성한 다음에는 iterative methods를 통해 solve (ex. GD, Langevin dynamics)
DDRM은 denoising diffusion generative model로, denoise하는 과정에서 measurements y와 inverse problem에 condition되어 sampling하게 된다. 또한 본 모델은 inverse problem의 posterior distribution을 학습할 수 있는 variational inference objective를 소개하며 결국 기본 unconditional denoising diffusion generative model의 objective와 동일하다는 것을 보여 H와 SVD만 변경할 수 있도록 하였다.
Background
Linear Inverse Problems
y = Hx + z
x : 복원할 signal
y : measurements (noisy obeservation)
z : Gaussian noise (stddev = sigma_y)
H : Degradation
= Noise observation y가 주어질때, x를 복원하는 문제
이때 x를 recover하기 위해서는 아래 posterior distribution을 구해 여기에서 반복적으로 sampling하면 된다.
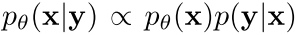
이때 p_thata(x) 는 inverse problem과 무관한 learned prior이고, p(y|x)는 y=Hx+z로 구할 수 있는 likelihood라고 볼 수 있다.
Denoising Diffusion Probabilistic Models (DDPMs)
Markov chain에 기반한 joint distibution을 정의:
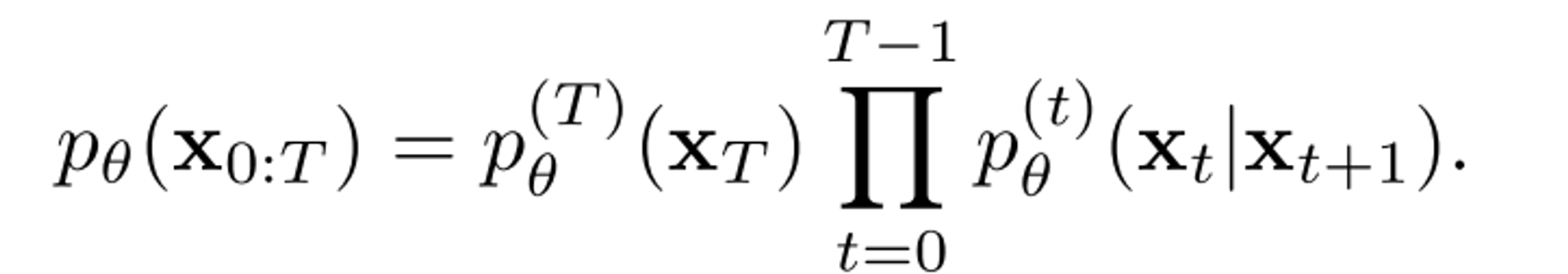
위 식에서 최종적으로 남는 샘플로는 오직 $x_0$가 된다.
DDIM에서는 diffusion model을 학습시키기위해 고정된 variational inference distribution을 다음처럼 정의했다. :
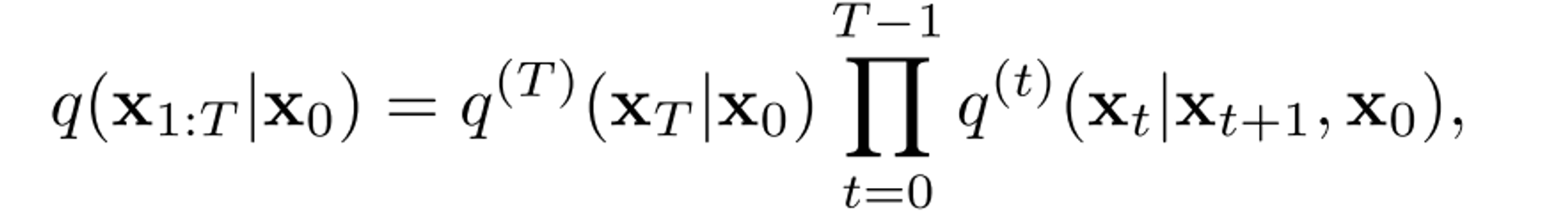
두 식 모두 conditional Gaussian distribution이고 x_t는 x_0로 표현될 수 있기때문에 ELBO objective를 정리하면 denoising autoencoder objective로 환원 가능하다.
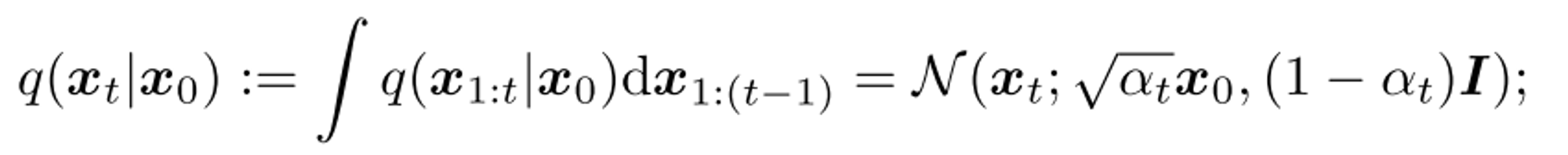
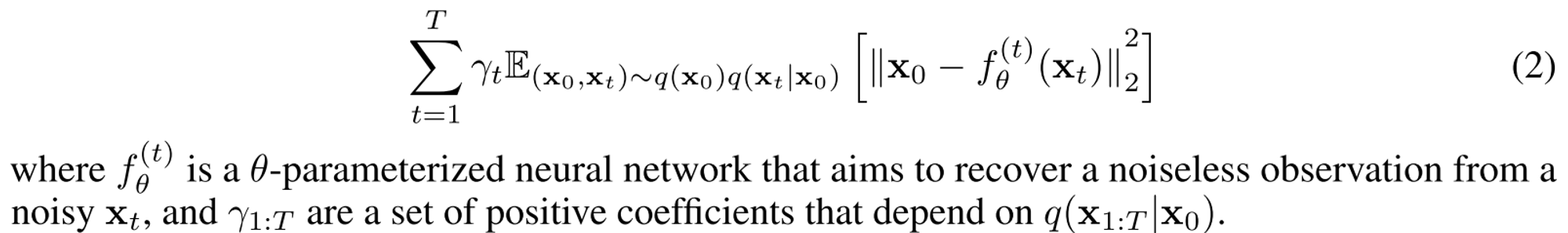
Denoising Diffusion Restoration Models
기본적으로 Supervied approaches는 효율적이지만 specific한 문제만 해결가능하고, unsupervised approaches는 비효율적이지만 general하게 사용 가능하다는 dilema가 존재하는데. DDRM은 supervised learning objectives에도 suit한 unsupervised solution을 제안한다는 점에서 유의미하다고 볼 수 있다.

[1] Variational Objective for DDRM
Linear inverse problem에 대한 condition y를 고려하도록 위에서 정의한 식을 수정하면 아래외 같다.
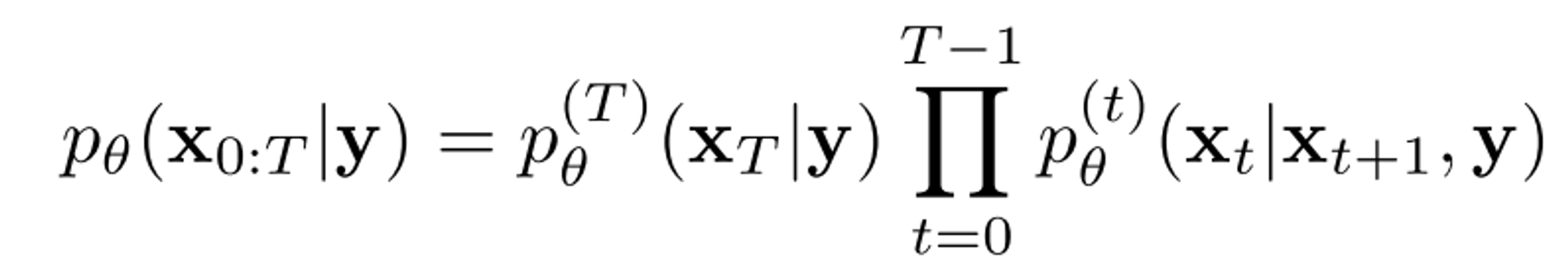
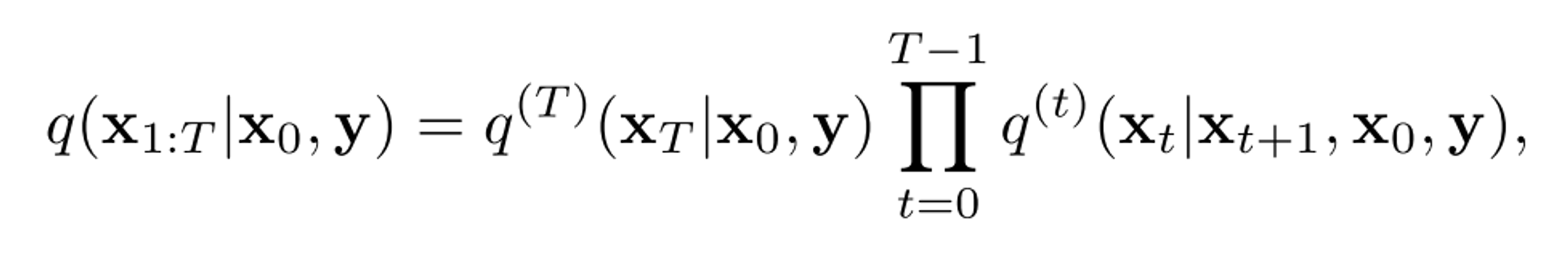

이때 q(xt|x0) = N(x0, σt^2 I) (0 = σ0 < σ1 <σ2 < . . . < σT)로 정의하는데,
이는 기존 DDPM, DDIM에서의 q(xt|x0)와 동일하다는 것을 보였다.

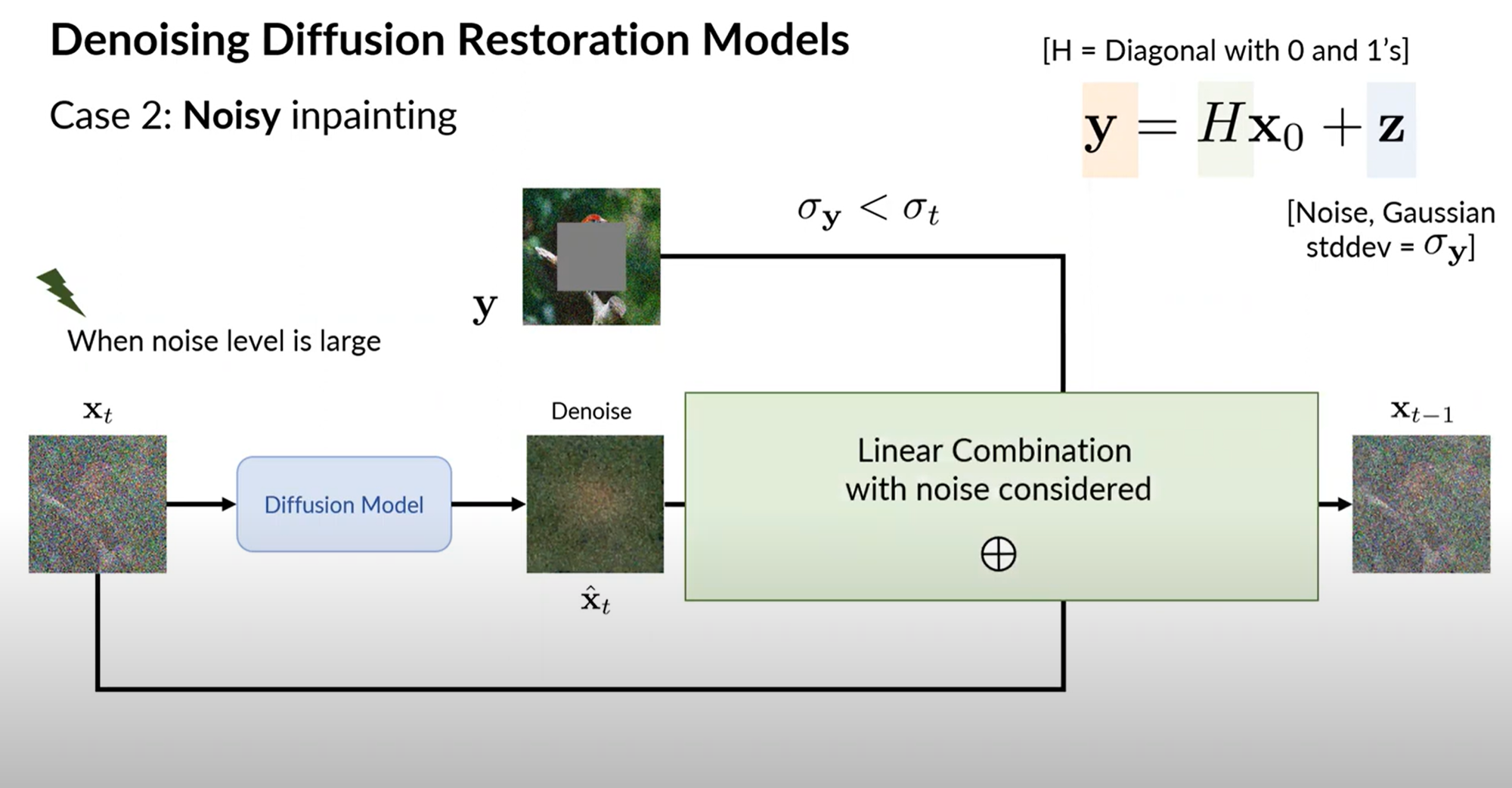
[2] A Diffusion Process for Image Restoration
SNIPS처럼 H의 SVD를 고려해 spectral space에서 diffusion을 진행한다. 이는 noisy한 measurements y의 noise와 diffusion 과정의 noise인 x_1:T를 같은 space에 두어서 처리하고, output인 x0가 measurements에 faithful할 수 있도록 해주기 위함이다.
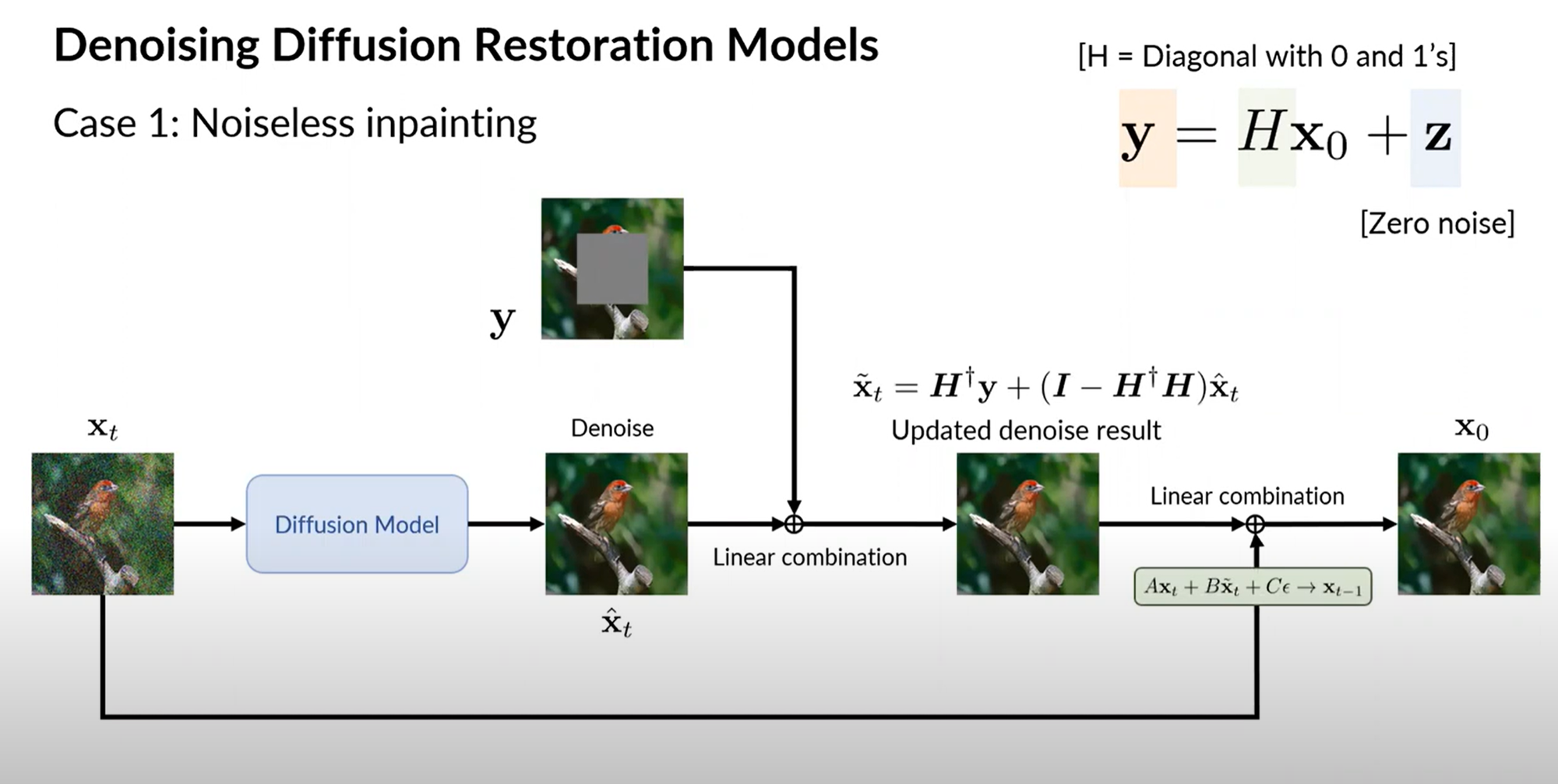
H=UΣV^T
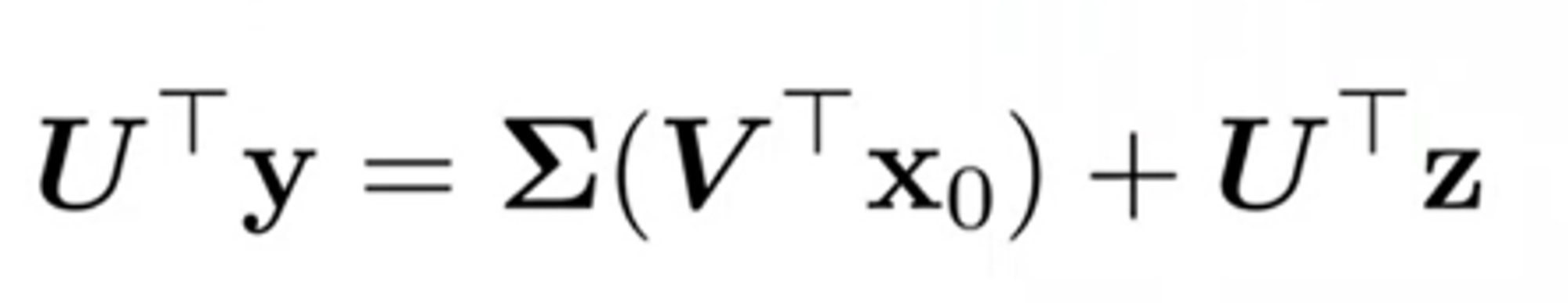
즉 noisy observation y에 없는 데이터를 x에서 확인해 diffusion process를 통해 synthesize하게 된다.
또한 y도 denoising process에 넣게되는데, inpainting을 예로 들면 missing pixel들을 model이 generate하고, 관찰된 y의 값들은 denoising하게 된다. (run denoising and inpainting in spectral space)
아래 notation들은 spectral space에서 정의된다 :
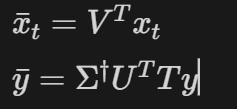
위 notation을 이용해 variational distribution을 정의하면 다음과 같다.
(1) Define qt as a series of Gaussian Conditionals
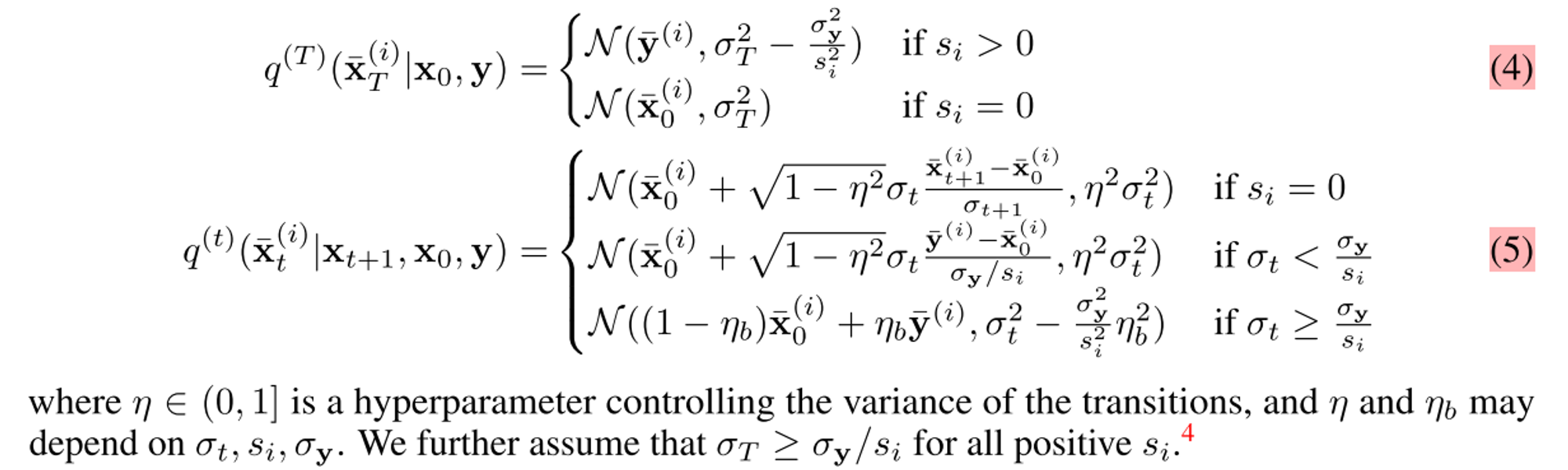
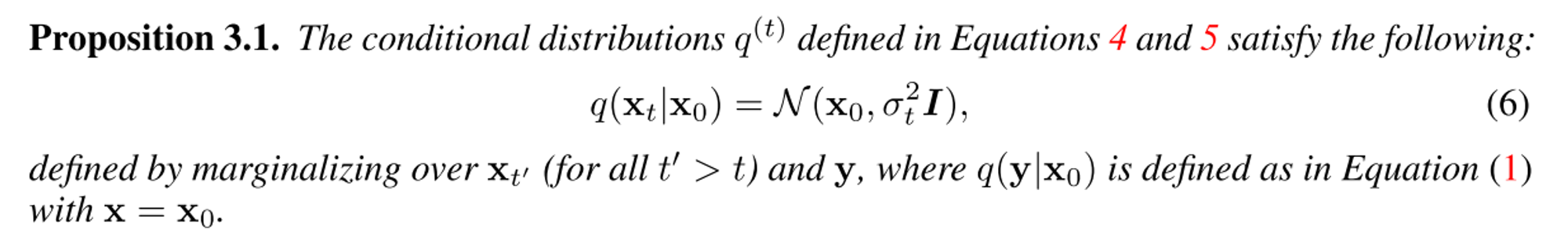
중요한 점은 spectral space에서 measurements의 noise level이 diffusion noise보다 클 경우 η를, 작을 경우 η_b를 hyperparamter로 하여 transitions의 variance를 조절한다.
1) spectral space에서 measurements의 noise level이 diffusion noise보다 작을 경우
- y를 denoising에 활용함 ⇒ xt, xt tilde, noise를 이용해 x_t-1을 구함.
- η_b를 hyperparamter로 하여 transitions의 variance를 조절
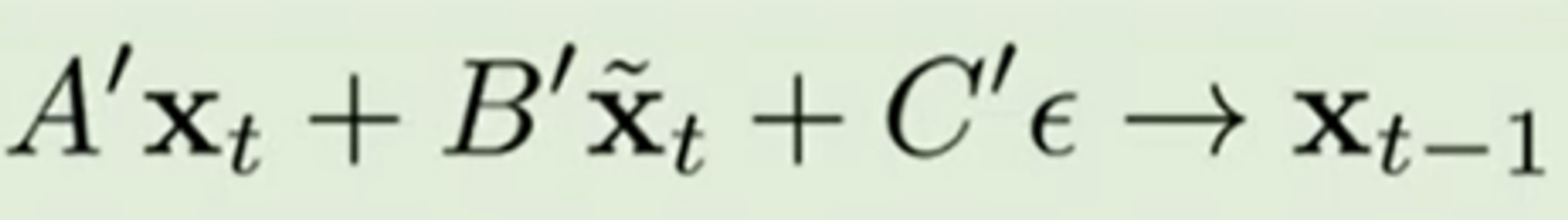
2) measurements의 noise level이 diffusion noise보다 큰 경우
- measurements y를 denoising에 활용하지 않음.
- η 를 hyperparamter로 하여 transitions의 variance를 조절
- 따라서 xt, xt hat, epsilon을 이용해 x_t-1을 구함. (=그냥 DDIM)
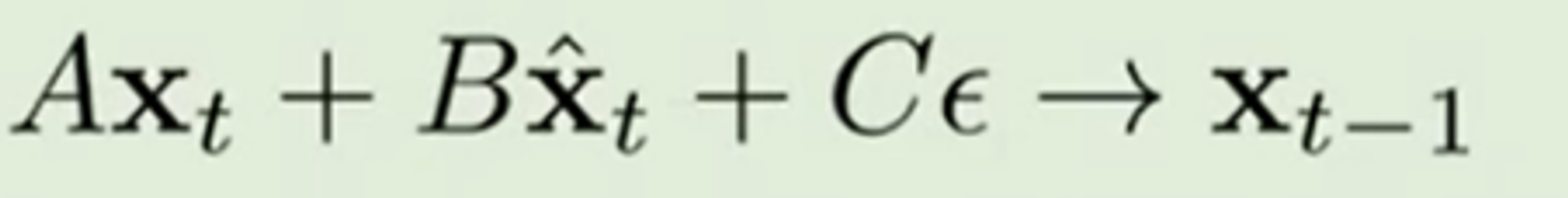
-> 즉 디퓨전 모델 시 차원 별 singular value에 따라 노이즈 레벨 측정하고 distribution을 다르게 설정하는 것이다. (Singular value를 이용해 추정한 Spectral space에서의 노이즈 레벨과 해당 time step의 노이즈 레벨을 비교, diffusion modeling을 차원의 특징에 따라 다르게 진행)
(2) Define p_{\theta} as a series of Gaussian conditionals
model f_theta(x_{t+1}, t+1)의 예측값을 $x_{\theta, t}$ 라 하자. (sample x_t+1과 t+1일때의 condition을 사용)
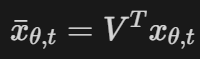
trainable parameter theta를 이용해 DDRM을 정의하면 다음과 같다
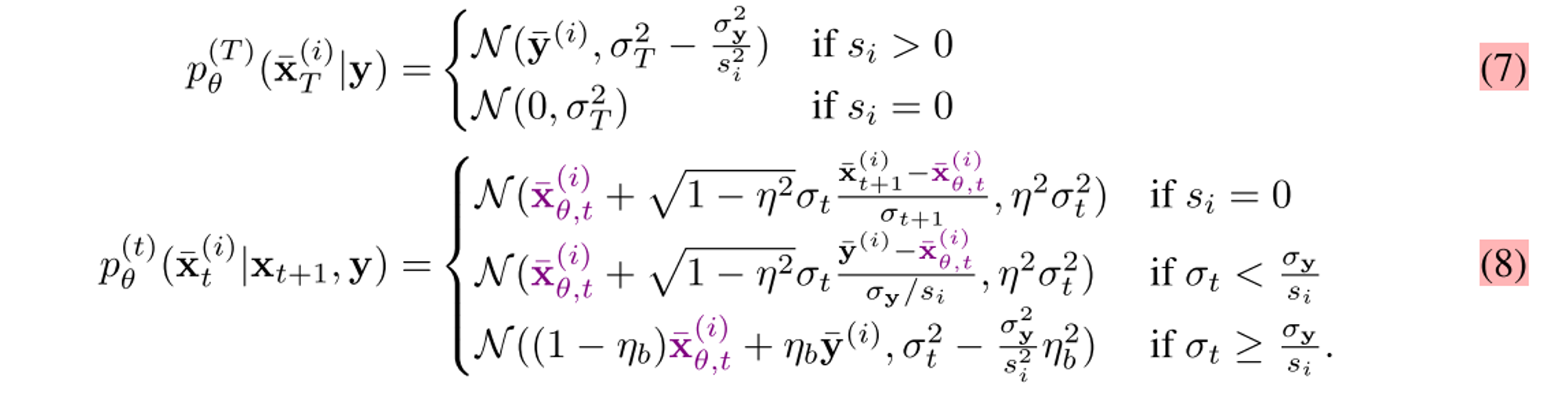
위 식은 그냥 (1)에서 x0 bar대신 모델의 예측값을 갖도록 하고, t=T일때는 0이 되도록 변경했다.
[3] Learning Image Restoration Models
우리는 [2]에서 p_thata, q를 sigma1:T, η, η_b로 정의할 수 있게 되는데
Inverse problem마다 H, $\sigma_y$가 주어지면 다른 모델을 학습시켜야하는데 이 방식으로 선택하게 되면 충분히 flexible하지 않기때문에, 본 논문에서는 DDRM의 optimal solution이 DDPM/DDIM의 optimal solution과 동일함을 보였다.

[4] Accelerate Algorithms for DDRM
DDRMM에서도 증가하는 $\sigma_{1:T}$에 대해서 denoising autoencoder objective를 구할 수 있기때문에 ddim등과 마찬가지로 skipping steps를 process에 적용할 수 있어서 알고리즘을 accelerate하는 것이 가능하다.
Experiment


Conclusion
DDRM은 general sampling-based linear inverse problem solver으로, unconditional/class-conditional diffusion generative models를 learned prior로 하고 있다. 그리고 DDPM은 다른 샘플링 베이스라인들과 비교했을때 매우 적은 수의 NFE(20)을 가졌고 다양한 상황들에 대해서 scalability를 가졌다(denoising, super-resolution, deblurring, inpainting, colorization). 핵심적으로 본 모델은 SVD를 활용하고, singular value를 이용해 추정한 Spectral space에서의 노이즈 레벨과 해당 time step의 노이즈 레벨을 비교한 다음 diffusion modeling을 차원의 특징에 따라 다르게 진행한다는 점에서 novelty가 있다.




