| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- ML
- ccdf
- face forgery detection
- fourmer
- Ai
- daod
- facenet
- deepfake detection
- f2dnet
- ddrm
- linear inverse problem
- image restoration
- neighboring pixel relationships
- focal detection network
- diffusion
- hqs-algorithm
- IR
- diffpir
- conditional diffusion
- unconditional generative models
- ssda-yolo
- ddpm
- stochastic contraction theory
- object detection
- Triplet
- pedestrian detection
- semi-supervied learning
- ddim
- ilvr
- unconditional ddpm
- Today
- Total
Stand on the shoulders of giants
[paper review] DPS (Diffusion Posterior Sampling For General Noisty Inverse Problems) 본문
[paper review] DPS (Diffusion Posterior Sampling For General Noisty Inverse Problems)
finallyupper 2024. 7. 14. 11:02Main Idea
대부분의 IR work들은 linear inverse problems에 집중한 반면, 본 논문은 posterior sampling을 통해서 noisy한 (non)linear inverse problems를 다룰수 있는 diffusion solver를 제안한다. 이를 통해 Gaussian이나 푸아송과 같은 여러가지 measurement noise statistics를 해결할 수있고, 그 외에 fourier phase retrival과 non-uniform deblurring과 같은 nonlinear inverse problem들을 효과적으로 다룰 수 있게 했다는 점에서 의미가 있다
Introduction
Inverse problems를 해결하기 위해서 diffusion models를 통해 학습한 prior를 활용하는데, score function과 같은 log density의 gradient를 활용하게 된다. (Inverse 문제에서는 forward measurement operator A와 detector noise n으로 구성된 measurement y를 통해 x를 복원하는 task이다. )
즉 필요한 것은 posterior distribution $p(x|y)$인데 이는 time t와 관련된 dependency 문제로 intractable하다.
이러한 문제점을 극복하기 위해 projection-based method들이 제안되었으나 nonlinear 상황이나 ill-posed일 경우 한계를 가졌다. 또한 SVD를 통해 spectral domain에서 diffusion을 사용하려는 시도의 경우에는 SVD computation도 비싸고 SVD를 사용하기 쉬운 inverse problems(ex. gaussian kernels)에서만 잘 작동하는 한계점을 있다. 그 외에 연구에서도 non-linear inverse problems에 대해 explore되지 않았다.
본 연구에서는 새로운 approximation 방법론을 통해서 posterior sampling이 tractable하도록 하여 noisy inverse problem을 해결했다. 또한 해당 framework의 경우 nonlinear inverse problem도 automic differentiation으로 gradients를 구할 수 있는 경우에 대해 해결할 수 있다. (Spectral domain을 사용하지 않고 image domain에서 해결)
Background
Score-based diffusion models
Itˆo stochastic differential equation (SDE)
1) Forward SDE
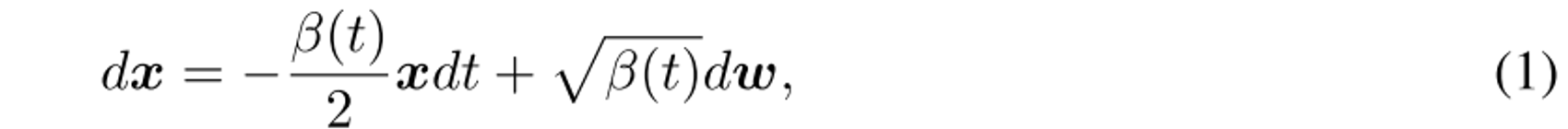
- β(t) : noise schedule (linearly increase)
- w : d-dim Wiener process
- Data distribution: x(0)~p_data ⇒ isotropic Gaussian x(T)~N(0, 1) (tractable)
2) Reverse SDE
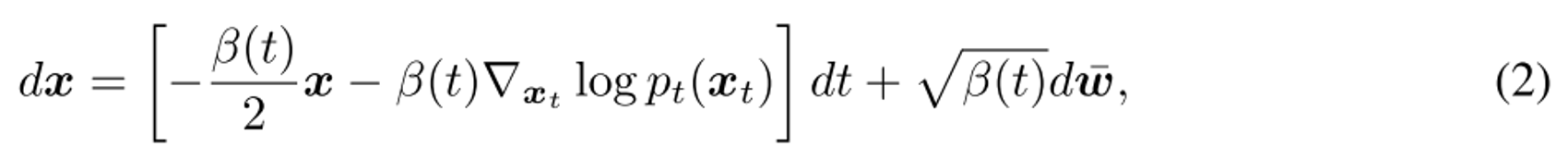
- dt : 반대방향으로의 time
- bar{w} : 반대방향으로의 Wiener process
해당 drift function(2)는 score function ∇xtlog pt(xt)으로 결정되고,
score function은 denoising score matching으로 학습된 nn인 s_theta 기반으로 approximated된다.


s_theta* term을 plug-in estimate로 사용하여 (2) 자리에 삽입한다.
본 논문에서는 generative model로 VP-SDE, DDPM을 사용하고 있다.
Inverse problem solving with diffusion models
inverse problem에서는 measurement y와 원본 x가 존재하고 y를 기반으로 x를 restore하게 되는데, x → y의 관계가 one-to-many이면 y에서 특정 x로 정확히 복원하는 것이 힘들기 때문에 ill-posed inverse probem이 된다.
[ Bayesian framework ] p(x) : prior, p(x|y): posterior 으로 정의해 Bayes’rule : p(x|y)=p(y|x)p(x)/p(y) 를 해결해 posterior를 구하여 sampling을 진행한다.
기존 (2)Reverse SDE를 변형해 Posterior p(x|y)를 p(x)자리에 대입해 posterior distribution에서 sampling하도록 설정하면 다음과 같아진다.
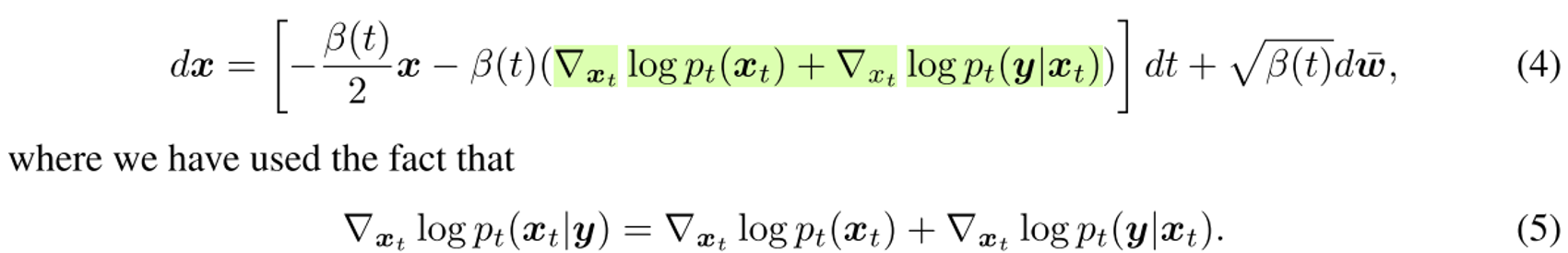
pt(x_t) : prior, pt(y|x_t) : likelihood (p(y)는 derivative를 하면 사라지기때문에.)
Term 1. ∇xt log pt(xt)
pre-trained score function sθ∗를 plug-in estimate로 사용해 대입
Term 2. ∇xt log pt(y|xt)
해당 term의 경우, y는 x0로부터 계산된 값이기 때문에 명백하게 dependent하지만 x_t와는 explicit dependence가 없기 때문에 (time t에서의 dependence가 존재하나) closed-form으로 해결하기 어렵다.


⇒ 본 연구에서는 우선 첫번째 term를 가지고(2) unconditional update를 진행하고, 이후 projection step을 거치면서 posterior distribution을 계산하고자 한다. (→ measurement consistency can be met when assuming n=0)
Diffusion Posterior Sampling (DPS)
Approximation of the likelihood
현재로썬 위에서 보인 바와 같이 p(y|xt)를 바로 구할수가 없기 때문에 y=A(x0) + n 관계식으로부터 얻을 수 있는 p(y|x0) ~ N (y|A(x0), sigma^2I)를 이용할 수 있도록 factorize하면 다음과 같다. :

이때 위에서 언급한 바와 같이 x_t와 y는 dependency가 없기 때문에 (conditionally independent) x_t를 지우고 표현할 수 있다. (즉 p(y|x0)를 이용할 수 있게되는 것!)
문제점은 p(x0|xt)가 diffusion model에서 항상 언급되었듯 intractable한데, VP-SDE, DDPM의 경우에는 (8)식을 기반으로 Tweedie’s approach를 통해서 해당 term을 구할 수 있다. * 논문의 기여점 *
Forward diffusion

Proposition 1.

⇒ Tweedie’s formula를 이용하게되면 (10)에 따라 x_t를 가지고 x_0 hat(empirical Bayes optimal posterior mean)을 구할 수 있다.

위에서도 언급했던 (7)식을 다르게 정리하면
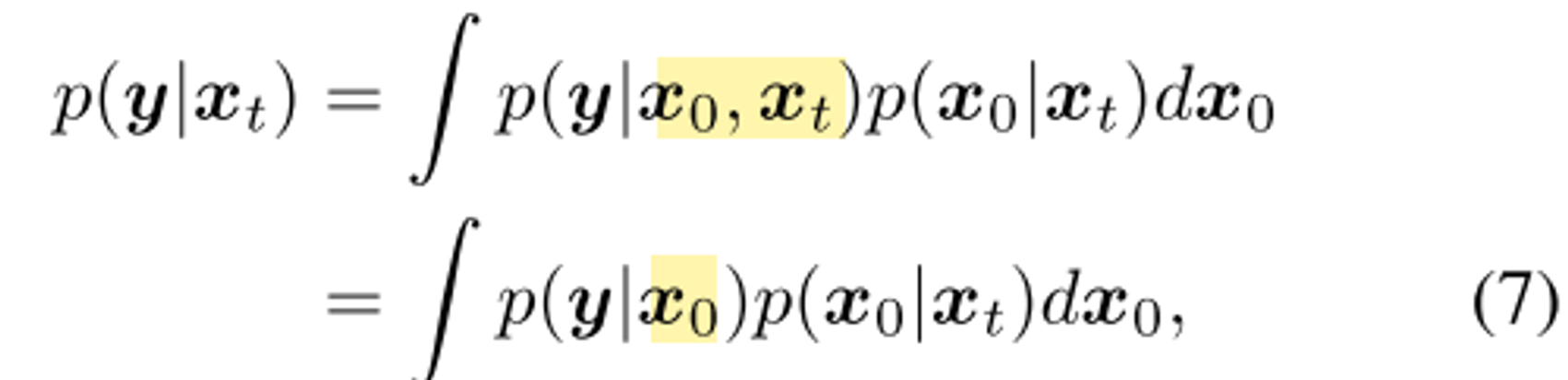
⇒ 다음처럼 적을 수 있고

즉 이렇게되면 x_t와 y 사이의 관계성을 얻을 수 있게 된다(= 2nd Term 해결).
이때 이렇게 approximate한 것은 Jensen’s inequality와 관련되어 있어 appoximation error를 구해볼 수 있다.

해당 definition을 통해서 y=A(x0) + n where n~N(0, sigma^2 I)일때 Jensen gap의 closed-form upper bound를 구할 수 있다.

(13) : (11)의 내용과 동일
Remark 2. Theorem 1에서 ∥∇xA(x)∥ 는 대부분의 inverse problems에서 finite하고 만약 m1도 finite하게 되면(일반적으로 finite) noise 가 점점 커질때 (σ → ∞, higher measurement noise) Jensen gap은 줄어들기 때문에 결과적으로 approximation error가 감소하게 된다.
즉 해석해보면 step을 점점 키울수록 p(y|x0 hat)으로 estimate한 것은 점점 p(y|xt)와 유사해지는 것이다.
뿐만 아니라 Theorem 1.에서는 n을 Gaussian distribution으로 정의하고 풀었으나 Poisson과 같은 다른 measurement distribution들에서도 Jensen gap을 정의할 수 있다.

Model Dependent Likelihood of the measurement
Gaussian noise

즉 해당 사실을 활용하면 두번째 term도 구할 수 있게 되고, 이를 바탕으로 기존 식을 다시 작성하면 posteior distribution을 구할수 있게 되는 것이다!
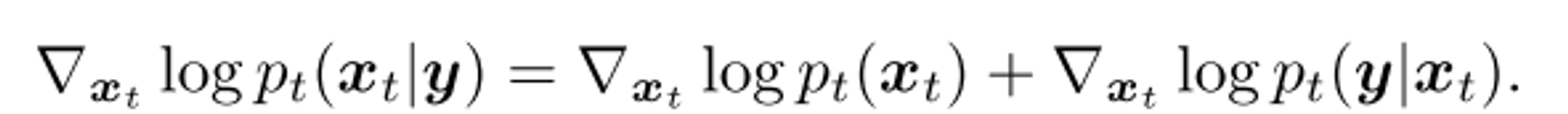

Poisson noise
Poisson noise도 gaussian noise와 같은 맥락으로 두번째 term을 계산하면 posterior distriution을 approximate할 수 있다.

이러한 증명에 따라, 본 연구에서는 posterior distribution에서 sampling할 수 있게 되기 때문에 알고리즘을 Diffusion Posterior Sampling (DPS)으로 이름짓게 된 것을 알 수 있다.
일반적인 기존 방법론들에서는 linear inverse problems만 해결했는데 (A(x) = Ax) 해당 모델은 non-linear operators A(.)에서도 사용이 가능하다. 이는 뒤의 실험에서 Fourier phase retrieval과 non-uniform deblurring과 관련해 실험해서 보였다.
Experiments
Dataset으로는 FFHQ 256x256, Imagenet 256x256을 사용
ImageNet에 쓰인 모델은 pre-trained된 diffusion model을 finetuning없이 바로 썼고 FFHQ 기반 diffusion model은 scratch부터 traning했다고 한다. 적용한 Tasks는 Super Resolution, Inpaint, Deblur이다.
Linear Inverse Problem
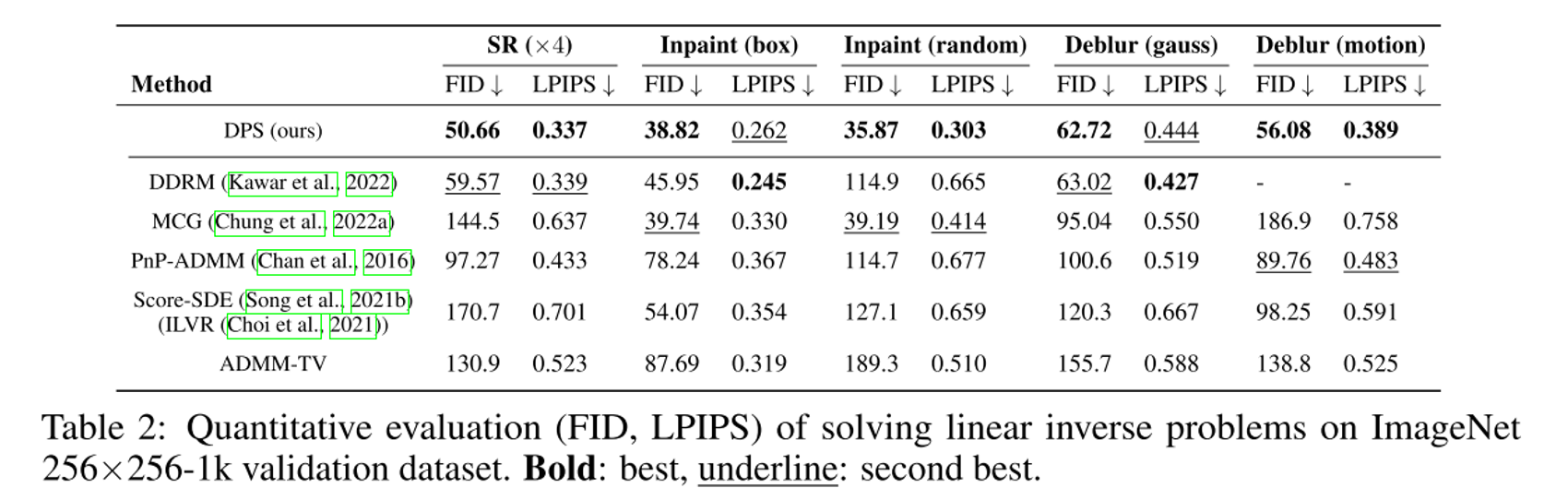
Gaussian measurements 기반의 linear inverse problems를 실험했다.
Measurement noise에 robust하다고 알려진 DDRM, PnP-ADMM과 비교 실험해보니 두 모델에 비해 해당 task들에서 좋은 성능을 보였음을 확인할 수 있다.
DDRM은 SVD에 기반한 방법론이기때문에 forward measurement matrix가 잘 설계될 수 있는 상황에 대해서만 문제를 잘 해결할 수 있어서 차원이 매우 낮은 image inpainting task나 (Gaussian blur가 아닌 motion blur 등) blurring에서 poor하게 perform했다. 이와 달리 DPS는 어떤 condition에 국한되지 않고 처리가 가능하다.



Nonlinear Inverse problems



실험 결과 phase retrieval problem에 대해서 정확하게 대부분의 high-frequency 정보들을 복원했다. Table을 보면 알 수 있듯 큰 차이로 기존 모델들(OSS, HIO, ER)보다 우월한 성능을 보였음을 확인할 수 있다.
Conclusion
본 논문은 일반적인 noisy inverse problems에 적용 가능한 DPS 전략을 제안해 매우 noisy하거나 nonlinear inverse problems인 경우에도 사용이 가능하다는점과, 기존 SOTA 모델들과 큰 차이로 좋은 성능을 냈다.




